Time series statistics

Library of often used functions for evaluating properties of time series or data arrays. See also Normalization.

correl(vars Data, int Length, function): var

Spearman correlation of the Data series with an arbitrary function. Used for the CTI, CCYI, and CCYIR indicators. Source in indicators.c; usage and description on Financial Hacker.

Correlation(vars Data1, vars Data2, int TimePeriod): var

Pearson's correlation coefficient between two data series over the given TimePeriod, in the range between -1..+1. A coefficient of +1.0, a "perfect positive correlation," means that changes in Data2 cause identical changes in Data1 (e.g., a change in the indicator will result in an identical change in the asset price). A coefficient of -1.0, a "perfect negative correlation," means that changes in Data2 cause identical changes in Data1, but in the opposite direction. A coefficient of zero means there is no relationship between the two series and that a change in Data2 will have no effect on Data1. This function can be also used to get the autocorrelation of a series by calculating the correlation coefficient between the original series and the same series lagged by one or two bars (series+1 or series+2).

Covariance(vars Data1, vars Data2, int TimePeriod): var

Covariance between two data series. Can be used to generate a covariance matrix f.i. for the markowitz efficient frontier calculation.

Fisher(vars Data): var

Fisher Transform; transforms a normalized Data series to a normal distributed range. The return value has no theoretical limit, but most values are between -1 .. +1. All Data values must be in the -1 .. +1 range, f.i. by normalizing with the AGC, Normalize, or cdf function. The minimum Data length is 1; a single var can be passed with the & operator, f.i. Fisher(&MyVariable). Source in indicators.c.

FisherInv(vars Data): var

Inverse Fisher Transform; compresses the Data series to be between -1 and +1. The minimum length of the Data series is 1; a single var can be passed with the & operator, f.i. FisherInv(&MyVariable). Source in indicators.c.

FisherN(vars Data, int TimePeriod): var

Fisher Transform with normalizing; normalizes the Data series with the given TimePeriod and then transforms it to a normal distributed range. Similar to a Normalize filter (see below), but more selective due to the normal distribution of the output. The return value has no theoretical limit, but most values are in the -1.5 .. +1.5 range. The minimum length of the Data series is equal to TimePeriod. The function internally creates series (see remarks). Source code in indicators.c.

FractalDimension(vars Data, int TimePeriod): var

Fractal dimension of the Data series; normally 1..2. Smaller values mean more 'jaggies'. Can be used to detect the current market regime or to adapt moving averages to the fluctuations of a price series. Requires a lookback period of twice the TimePeriod. Source in indicators.c.

Gauss(vars Data, int TimePeriod): var

Gauss Filter, returns a weighted average of the data within the given time period, with the weight curve equal to the Gauss Normal Distribution. Useful for removing noise by smoothing raw data. The minimum length of the Data series is equal to TimePeriod, the lag is half the TimePeriod. Source in indicators.c.

Hurst (vars Data, int TimePeriod): var

Hurst exponent of the Data series; between 0..1. The Hurst exponent measures the 'memory' of a series. It quantifies the autocorrelation, i.e. the tendency either to revert to the mean (Hurst < 0.5) or to continue trending in a direction (Hurst > 0.5). This way the Hurst exponent can detect if the market is in a trending state. The TimePeriod window (minimum 20) must have sufficient length to catch the long-term trend; the lookback period must be at least twice the TimePeriod. The function internally creates series (see remarks). Source in indicators.c.

LinearReg(vars Data, int TimePeriod): var

Linear Regression, also known as the "least squares moving average" (LSMA). Linear Regression attempts to fit a straight trendline between several data points in such a way that the distance between each data point and the trendline is minimized. For each point, the straight line over the specified previous bar period is determined in terms of y = b + m*x, where y is the price and x the bar number starting at TimePeriod bars ago. The formula for calculating b and m is then

m = (nΣxy - ΣxΣy) / (nΣx² - (Σx)²)
b = (Σy - bΣx) / n

where n is the number of data points (TimePeriod) and Σ is the summation operator. The LinearReg function returns b+m*(TimePeriod-1), i.e. the y of the current bar.
Source in ta-lib.zip. For higher order regression or for evaluating the regression value at past or future bars, use polyfit / polynom. For logistic regression with multiple variables, use the advise(PERCEPTRON,...).

LinearRegAngle(vars Data, int TimePeriod): var

Linear Regression Angle. Returns m converted to degrees. Source in ta-lib.zip. Due to the arbitrary x and y units of a price chart, the angle is a mostly useless parameter, although held in high esteem by Gann believers.

LinearRegIntercept(vars Data, int TimePeriod): var

Linear Regression Intercept. Returns b. Source in ta-lib.zip.

LinearRegSlope(vars Data, int TimePeriod): var

Linear Regression Slope. Returns m as data difference per bar. Source in ta-lib.zip.

MatchIndex(vars Data, var Reference, int Period): int

Index of the Data value closest to Reference over the specified Period. 0 = best match is at current bar, 1 = at one bar ago, and so on. If the Data series was shifted (+N), add the offset N to the returned index for getting the number of bars passed since the best match. Source in indicators.c.

MaxIndex(vars Data, int Period): int

Index of highest Data value over the specified Period.. 0 = highest value is at current bar, 1 = at one bar ago, and so on. If the series was shifted (+N), add the offset N to the returned index for getting the number of bars passed since the lowest Data value. Source in ta-lib.zip.

MaxVal(vars Data, int Period): var

Highest Data value over the specified Period. Source in ta-lib.zip.

Median(vars Data, int Period): var

Median Filter; sorts the elements of the Data series and returns their middle value within the given Period. Useful for removing noise spikes by eliminating extreme values. The minimum length of the Data series is equal to Period, the lag is half the Period. Source in ta-lib.zip. See also Percentile.

MinIndex(vars Data, int Period): int

Index of the lowest value over a specified period; 0 = lowest value is at current bar, 1 = at one bar ago, and so on. If the series was shifted (+N), add the offset N to the returned index for getting the number of bars passed since the lowest Data value. Source in ta-lib.zip.

MinVal(vars Data, int Period): var

Lowest value over a specified period. Source in ta-lib.zip.

MinMax(vars Data, int Period): var

Lowest and highest values over a specified period. Result in rMin, rMax. Source in ta-lib.zip.

MinMaxIndex(vars Data, int Period): int

Indexes of lowest and highest values over a specified period. Result in rMinIdx, rMaxIdx. 0 = current bar, 1 = one bar ago, and so on. Source in ta-lib.zip.

Mode(vars Data, int TimePeriod, int Steps): var

Most frequent Data value within TimePeriod. For this the Data range is divided into Steps separate ranges, and the number of values that fall into a range is counted. The function returns the value with the highest count. Source in indicators.c.

Moment(vars Data, int TimePeriod, int N): var

The statistical moment N (1..4) of the Data series section given by TimePeriod. The first moment is the mean, second is variance, third is skewness, fourth ist kurtosis. The standard deviation is the square root of the second moment. The mean is stored in rMean. See also SemiMoment. Source in indicators.c.

NumAbove(vars Data, int Length, var Theshold): var

Number of Data elements above the given Threshold within the Length, from 0 to Length. Source in indicators.c.

NumInRange(vars Low, vars High, var Min, var Max, int Length): var

Number of data ranges, given by their Low and High values, that lie completely inside the interval from Min to Max within the given Length. Can be used to calculate the distribution of prices or candles. Low and High can be set to the same value for counting all values in the interval, or swapped for counting all candles that touch the interval. Returns a value of 1..Length. Source in indicators.c. See also PercentRank.

NumRiseFall(vars Data, int TimePeriod): var

Length of the last streak of rising or falling values in the Data series, back to the given TimePeriod. For a rising sequence its length is returned, for a falling sequence the negative length (f.i. -3 when Data[3] < Data[2] > Data[1] > Data[0]). Range: 1..TimePeriod-1. See the RandomWalk script for an example. Source in indicators.c.

NumUp(vars Data, int TimePeriod, var Theshold): var

NumDn(vars Data, int TimePeriod, var Theshold): var

Number of upwards or downwards Data changes by more than the given Threshold within the TimePeriod, from 0 to TimePeriod-1. See also SumUp, SumDn. Source in indicators.c.

Percentile(vars Data, int Length, var Percent): var

Returns the given percentile of the Data series with given Length; f.i. Percent = 95 returns the Data value that is above 95% of all other values. Percent = 50 returns the Median of the Data series.

PercentRank(vars Data, int Length, var Value): var

The opposite of Percentile: Returns the percentage of Data values within the given Length that are smaller or equal than the given Value; returns 100 when Value is the greatest in the data range. Can transform any series to a range of 0..100. See also NumInRange.

R2(vars Data, int Length): var

Coefficient of determination (+1...-1); similarity of the Data series with a straight line through its end points. At 1 the data series is equivalent to a straight line, at 0 or below even the mean of the data is a better fit to the straight line than the real data series.

SemiMoment(vars Data, int TimePeriod, int N): var

The statistical moment N (1..4) of the Data series section given by TimePeriod, using only data points at or below the mean. The first moment is the mean, the second is the semivariance, third is downside skew, and fourth is downside kurtosis. The mean is stored in rMean. The semideviation (downside deviation) is the square root of the semivariance, and is often considered a better measure of risk than the standard deviation. See also Moment. Source in indicators.c.

ShannonGain(vars Data, int TimePeriod): var

Expected logarithmic gain rate of the Data series in the range of about +/-0.0005. The gain rate is derived from the Shannon probability P = (1 + Mean(Gain) / RootMeanSquare(Gain)) / 2, which is the likeliness of a rise or fall of a high entropy data series in the next bar period. A positive gain rate indicates that the series is more likely to rise, a negative gain rate indicates that it is more likely to fall. The zero crossover could be used for a trade signal. Algorithm by John Conover. Source in indicators.c.

ShannonEntropy(vars Data, int Length, int PatternSize): var

Entropy of patterns in the Data series, in bit; can be used to determine the 'randomness' of the data. PatternSize (2..8) determines the partitioning of the data into patterns of up to 8 bit. Each Data value is either higher than the previous value, or it is not; this is a binary information and constitutes one bit of the pattern. The more random the patterns are distributed, the higher is the Shannon entropy. Totally random data has a Shannon entropy identical to the pattern size. Algorithm explained on the Financial Hacker blog; source in indicators.c.

Spearman(vars Data, int TimePeriod): var

Spearman's rank correlation coefficient; correlation between the original Data series and the same series sorted in ascending order within TimePeriod (1..256). Returns the similarity to a steadily rising series and can be used to determine trend intensity and turning points. Range = -1..+1, lag = TimePeriod/2. For usage and details, see Stocks & Commodities magazine 2/2011. Source in indicators.c.

StdDev(vars Data, int TimePeriod): var

Standard Deviation of the Data series in the time period, from the ta-lib; accuracy = 0.0001. For long time periods, higher accuracy, or for downside deviation, use the square root of the second Moment or SemiMoment.

Sum(vars Data, int Length): var

Sum of all Data elements up to the given Length. Source in ta-lib.zip.

SumUp(vars Data, int Length): var

SumDn(vars Data, int Length): var

Sum of all upwards or downwards Data changes up to the given Length. See also NumUp, NumDn. Source in indicators.c.

SumSq(vars Data, int Length): var

Sum of the squares of all Data elements up to the given Length. Source code in indicators.c.

TSF(vars Data, int TimePeriod): var

Time Series Forecast. Returns b + m*(TimePeriod), the Linear Regression forecast for the next bar.

Variance(vars Data, int TimePeriod): var

Variance of the Data series in the time period, accuracy = 0.0001. Source in ta-lib.zip. For long time periods, higher accuracy, or for downside variance, use the second Moment or SemiMoment.

Standard parameters:

TimePeriod	The number of bars for the time period of the function, if any; or 0 for using a default period.
Length	The length of the Data series.
Data	A data series, in reverse time order, usually derived from the price functions price(), priceC() etc.. Alternatively a user created series or any other double float array with the given minimum length can be used. If not mentioned otherwise, the minimum length of the Data series is TimePeriod. Some functions require a second data series Data2.

Usage example:

Volatility(Prices,20) calculates the standard volatility of a daily price series over the last 20 days.

Remarks:

The TA-Lib function prototypes are defined in include\functions.h. The C source code of all included TA-Lib indicators is contained in Source\ta_lib.zip and can be studied for examining the algorithms. Some TA-Lib indicators that originally didn't work properly - such as Correlation or SAR - have been replaced by working versions. The C source code of most additional indicators that are not part the the TA-Lib is contained in Source\indicators.c.
TA-Lib indicators can only be used between INITRUN and EXITRUN, since TA-Lib and series management are released at end of the session. This restriction does not apply when the STRAIGHT flag is set.
TimeFrame affects subsequent data series and thus also affects all indicators that use the data series as input. The TimePeriod is then not in Bar units, but in time frame units. TimeFrame has no effect on indicators that do not use data series.

Examples:

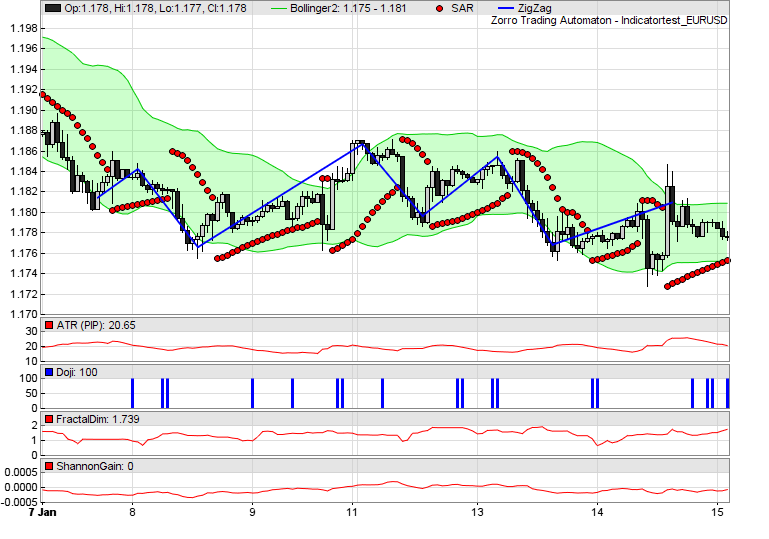
// plot some indicators
function run()
{
  set(PLOTNOW);
  var* Price = series(price());
	
// plot Bollinger bands
  BBands(Price,30,2,2,MAType_SMA);
  plot("Bollinger1",rRealUpperBand,BAND1,0x00CC00);
  plot("Bollinger2",rRealLowerBand,BAND2,0xCC00FF00);
  plot("SAR",SAR(0.02,0.02,0.2),DOT,RED);
  ZigZag(Price,20*PIP,5,BLUE);
	
// plot some other indicators	
  plot("ATR (PIP)",ATR(20)/PIP,NEW,RED);
  plot("Doji",CDLDoji(),NEW+BARS,BLUE);
  plot("FractalDim",FractalDimension(Price,30),NEW,RED);
  plot("ShannonGain",ShannonGain(Price,40),NEW,RED);
}