Mean/Variance Optimization
markowitz (var* Covariances, var* Means, int N, var Cap) : var
markowitz (var* Covariances, var* Means, int N, var* Caps) : var
Performs a mean / variance optimization (MVO) using the
algorithm from the 1959 publication Portfolio Selection: Efficient
Diversification of Investments by Harry M. Markowitz;
also referred to as modern portfolio theory
(MPT). The fucntion calculates the optimal distribution of capital
among a portfolio of assets or algorithms for achieving a given total return or
variance. The algorithm starts with assigning all capital to the component with
the highest return. It then adds or removes more components step by step,
calculating the optimal return/variance combination on any step.
The
efficient frontier
is a line consisting of corner points in a return over variance plot. At any
corner point the portfolio composition changes by adding or removing one or
several components. Between the corner points the included components don’t
change, only their capital allocation changes linearly. Connecting all corner
points with lines establishes the efficient frontier with the
maximum return for any given variance (see image).
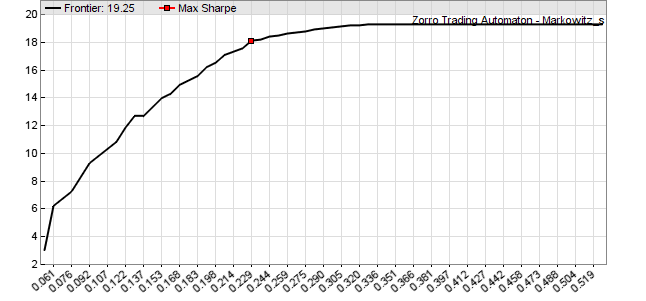
Efficient frontier of an ETF portfolio, x axis = variance,
y axis = annual return in %
Parameters:
| Covariances |
A var[N*N] array containing the covariance matrix
of the component returns. |
| Means |
A var[N] array containing the mean of the component
returns. |
| N |
Number of components, at least 3. |
| Cap |
Weight cap in 0..1 range; soft weight limit of a
single asset at the minimum variance point, or 0 for no
weight cap. |
| Caps |
A var[N] array containing individual weight limits
in 0..1 range, or 0 for no weight cap.
|
Returns
Variance at the efficient frontier point with the best Sharpe Ratio (i.e. return
divided by standard deviation), or 0 if the efficient frontier
could not be calculated. The efficient frontier line segments are internally
stored for subsequent markowitzReturn or
markowitzVariance
calls.
markowitzReturn (var* Weights, var Variance) : var
Calculates the return and the optimal capital allocation weights for a given
variance at a previously calculated efficient frontier. The markowitz()
function must be called before for calculating the frontier.
markowitzVariance (var* Weights, var Return) : var
Calculates the variance and the optimal capital allocation for a given return at
a previously calculated efficient frontier. The markowitz()
function must be called before for calculating the frontier.
Parameters:
| Weights |
A var[N] array to be filled with the capital
allocation weights of the N portfolio components. The
sum of the weights is 1. Pass 0 when
no weights are needed.
|
| Variance |
The desired variance. When below the lowest variance, the return and
weights at the left end of the efficient frontier are returned. |
| Return |
The desired return. When below the lowest return of the efficient
frontier, the variance and weights at the left end of the efficient
frontier are returned.
|
Returns
The optimal portfolio return at the given variance, or vice versa..
Modifies
Weights - set to the capital allocation weights.
Remarks:
- For getting the minimum variance point, call markowitzReturn
with Variance at 0. For maximum Sharpe
ratio, call markowitzReturn with the Variance
returned by markowitz(). For the maximum return point at
the right side of the diagram, call markowitzReturn with
Variance
at 1. For the maximum and minimum variances, call
markowitzVariance
with a return value above or below the maximum and minimum portfolio return.
- Markowitz weights can be used alternatively to
OptimalF
factors for allocating capital to a portfolio system. Unlike
OptimalF, they require only a relatively short time horizon and
thus can be adapted during live trading. For a long-term ETF rotation
strategy, use the last year price returns of the ETFs (see example) and
recalculate their markowitz weights every 4 weeks.
- For converting weights to asset amounts, multiply the weights with your
budget and divide by asset prices.
- For calculating the returns of portfolio components with currently zero
weight in real time, use phantom trades.
- It is often recommended to limit the asset weights with the Cap
or Caps parameter (f.i. 0.33 for 33%
maximum weight) for getting a higher portfolio diversification. This makes
the portfolio more stable and usually produces better out-of-sample results.
The weight cap can be exceeded when it is too small and the resulting
weights don't sum up to 1. For useful results, the weight cap should be at
least two or three times the 1/N minimum.
- MVO fails when there is no point on the efficient frontier that
represents the portfolio, for instance when all means are negative. This can
lead to weights of zero or to a total weight less than 1.
- Applications of the markowitz function are described in
the Financial Hacker article
Get Rich Slowly.
- The Z8 and Z10 trading systems use this
function for calculating optimal portfolio compositions. For other ways of
allocating capital, see the OptimalF,
distribute, and knapsack algorithms.
Example:
#define N 10 // 10 assets
#define DAYS 252 // 1 year
vars Returns[N];
var Means[N];
var Covariances[N][N];
function run()
{
BarPeriod = 1440;
StartDate = 20150101;
LookBack = DAYS;
string Name;
int n = 0;
while(Name = loop(.../*list of some assets*/ ... ))
{
asset(Name);
Returns[n] = series((price(0)-price(1))/price(1));
Means[n] = SMA(Returns[n],DAYS);
n++;
}
int i,j;
if(!is(LOOKBACK))
{
// generate covariance matrix
for(i=0; i<N; i++)
for(j=0; j<N; j++)
Covariances[i][j] = Covariance(Returns[i],Returns[j],DAYS);
// calculate efficient frontier
var OptimalV = markowitz(Covariances,Means,N);
printf("\nBest daily return %.3f %% at variance %.4f",
100*markowitzReturn(0,OptimalV),OptimalV);
// plot the frontier
for(i=1; i<70; i++) {
var VStep = i*OptimalV*0.03;
var Return = markowitzReturn(0,VStep);
plotBar("Frontier",i,VStep,Return,LINE|LBL2,BLACK);
}
plotGraph("Max Sharpe",1./0.03,markowitzReturn(0,OptimalV),SQUARE,RED);
PlotScale = 6;
PlotHeight1 = 300;
quit("");
}
}
See also:
OptimalF, Covariance,
distribute, knapsack
► latest version online

