Basic Trigonometry
There are six basic trigonometric functions. Consider a right-angled triangle, one of whose other angles is x as in the figure below: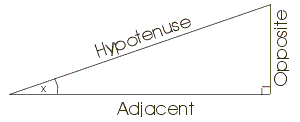
The basic functions are defined in terms of the length of the Hypotenuse (the longest side), the side Opposite the angle x, and the side Adjacent to angle x.
The sine of x, written as sin(x) is defined as:
| sin (x) | = | Opposite |
| Hypotenuse |
The cosine of x, written as cos(x) is defined as:
| cos (x) | = | Adjacent |
| Hypotenuse |
The tangent of x, written as tan(x) is defined as:
| tan (x) | = | Opposite |
| Adjacent |
Note that tan(x) is undefined where x = 0.
Using these functions, if an angle and the length of one side of a right-angled triangle are known, the length of the other two sides can easily be calculated.
| For angles between 90 and 180 degrees: sin(x) == sin(Π - x) cos(x) == -cos(Π - x) tan(x) == -tan(Π - x) |
|
| For angles between 180 and 270 degrees: sin(x) == - sin(Π + x) cos(x) == cos(Π + x) tan(x) == - tan(Π + x) |
For angles between 270 and 360 degrees: sin(x) == -sin(2Π-x) cos(x) == -cos(2Π-x) tan(x) == tan(2Π-x) |
The other three functions are the secant, cosecant, and cotangent - these are the reciprocal of the sine, cosine and tangent respectively. This is important, because the notation sin-1(x) is used to indicate the inverse sine function, or arc sine - that is, the angle whose sine is x. Similar notations apply to the arc cosine and arc tangent. Quick examination of the table above shows that the arc functions can deliver multiple answers for any given value - physical examination of the problem is usually required in order to determine which range the angle falls into.
Some useful functions:
|
tan(x) = sin(x) / cos(x) |
|
sin(x-y) = sin(x) cos(y) - cos(x) sin(y) |
|
cos(x+y) = cos(x) cos(y) - sin(x) sin(y) |
|
cos(x-y) = cos(x) cos(y) + sin(x) sin(y) |
|
tan(x+y) = (tan(x) + tan(y)) / (1 - tan(x) tan(y)) |
|
tan(x-y) = (tan(x) - tan(y)) / (1 + tan(x) tan(y)) |
By substituting x = y in the above formulae, we obtain:
|
sin(2x) = 2 sin(x) cos(x) |
|
cos(2x) = cos2(x) - sin2(x) |
|
tan(2x) = 2 tan(x) / (1 - tan2(x)) |